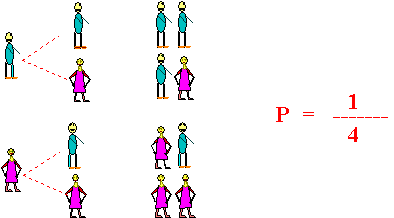|
|
|
|
PROBABILITÀ Modulo didattico Umberto Tenuta
<<È
veramente straordinario che una scienza, la quale ebbe
origine dall'esame dei giochi d'azzardo, dovesse assurgere al rango
di uno dei più importanti fondamenti della conoscenza umana>> (LAPLACE)
<<Oggi la fisica atomica e la fisica
quantistica portano a constatare come nel campo dei fenomeni
microscopici elementari non sia più valido il principio deterministico
della meccanica classica, nel senso che noi possiamo conoscere solo
la probabilità che una
determinata particella si trovi in una determinata zona dello
spazio, con una determinata velocità. Pertanto, la nostra
conoscenza del mondo reale è solamente probabilistica
e non deterministica>>(A.PICCATO)
<<Viviamo in un mondo di incertezze ed il
futuro cittadino deve essere preparato a far fronte ad esso in modo
corretto ed efficace>> (FISCHBEIN)
<<Per interpretare (la realtà) criticamente
e per intervenire consapevolmente su essa>> è
necessaria anche un'alfabetizzazione probabilistica.
Logica a due valori = vero/falso
Logica a più valori = vero/falso/probabile
Logica a più
valori anche come educazione alla comprensione degli altri (RICME)
OBIETTIVI POSTI DAI PROGRAMMI
DEL 1985
·
Iniziazione
informale al pensiero probabilistico
·
Pensiero
in situazione di incertezza
·
Elaborazione di giudizi e di
previsioni in situazioni di incertezza ovvero
·
Analisi razionale delle
situazioni di incertezza
INDICAZIONI DIDATTICHE Processo
lento e graduale, muovendo dalle
espressioni "forse
¾ è possibile ¾ è sicuro-non so ¾ è impossibile"
usate, in
modo significativo e coerente, in situazioni problematiche tratte
dalla vita reale e dal gioco <<Molti giochi hanno carattere aleatorio e
ricorrono alla sorte per l'assegnazione di particolari ruoli.
L'abilità del giocatore consiste nel saper scegliere, fra le
varie mosse possibili, quella che offre maggiori possibilità di
vittoria; si tratta dunque di condurre l'alunno a compiere
confronti di probabilità. Ciò può essere fatto dapprima in
termini più vaghi, e poi in situazioni ben schematizzate>>
CONCETTI FONDAMENTALI EVENTO = AVVENIMENTO
SPAZIO DEGLI EVENTI =
NUMERO DEI CASI POSSIBILI
CASI
FAVOREVOLI = EVENTI CHE DI VOLTA IN
VOLTA SI POSSONO VERICARE
PROBABILITÀ
=
RAPPORTO FRA IL NUMERO DEI CASI FAVOREVOLI
ED
IL NUMERO DEI CASI POSSIBILI IN SITUAZIONI ALEATORIE SIMMETRICHE
(CONCEZIONE
CLASSICA)
LA
PROBABILITÀ DI UN EVENTO È
IL VALORE DELLA
FREQUENZA AD ESSO RELATIVA QUANDO IL NUMERO DELLE PROVE
VENGA GIUDICATO SUFFICIENTEMENTE ELEVATO
(CONCEZIONE FREQUENTISTA)
EQUIPROBABILITÀ = PARI POSSIBILITÀ /
SITUAZIONI EQUIPOSSIBILI (SITUAZIONI
ALEATORIE SIMMETRICHE)
LANCIO DI UNA MONETA
ESTRAZIONE DI UNA
PALLINA
NASCITA DI DUE FIGLI
MASCHI
ESTRAZIONE DI DADI
ESERCITAZIONI OBIETTIVO PSI.1.
(1° CICLO) <<IN
SITUAZIONI PROBLEMATICHE CONCRETE TRATTE DALLA VITA REALE E DAL
GIOCO, USARE IN MODO SIGNIFICATIVO E COERENTE LE ESPRESSIONI: FORSE,
È POSSIBILE, È SICURO, NON SO, È IMPOSSIBILE ECC.>> È
opportuno suddividere l'obiettivo nei seguenti quattro
obiettivi specifici: 1° OBIETTIVO SPECIFICO (SI/NO): far acquisire i
concetti di sicuro/certo/vero e di non
vero/impossibile/falso -inventa
situazioni problematiche concrete tratte dalla vita reale e dal
gioco in cui si possano usare in modo significativo e coerente le
espressioni: sicuro/certo/vero
(SI)
e non
vero/impossibile/falso (NO) Ad esempio: -Oggi è venerdì? RISPOSTA:
si/no (vero/non vero)
-In questo momento siamo a scuola? RISPOSTA:
si/no (vero/non vero)
2° OBIETTIVO SPECIFICO (NON SO): far acquisire i
concetti di non so/incerto -inventa
situazioni problematiche concrete tratte dalla vita reale e dal
gioco in cui si possano usare in modo significativo e coerente le
espressioni: non
so/incerto Ad esempio: -Come si chiama il signore che attraversa la
strada? RISPOSTA:
non so
-Che cosa c'è scritto a pagina 25 di questo libro?
RISPOSTA:
non so
3° OBIETTIVO SPECIFICO (FORSE): <<In
situazioni problematiche concrete tratte dalla vita reale e dal
gioco, usare in modo significativo e coerente le espressioni: forse,
è possibile Ad esempio:
-nell'urna ci son palline rosse, verdi e blu. Se ne
estraiamo una, può essere rossa?
RISPOSTA: è
possibile, ma non sicuro
-oggi è nuvoloso: Domani pioverà?
RISPOSTA: forse sì.
4° OBIETTIVO SPECIFICO (SI-NO-FORSE): -inventa
situazioni problematiche concrete tratte dalla vita reale e dal
gioco in cui si possono usare in modo significativo e coerente le
espressioni: forse,
è possibile, è sicuro, non so, è impossibile
N.B. L'evento possibile/probabile/incerto si colloca tra l'evento
impossibile/falso/non vero e l'evento vero/certo/sicuro:
AVVIO AL CALCOLO DELLE PROBABILITÀ:
VALUTAZIONE GLOBALE I passaggi dal vero al falso, dal certo
all'impossibile... non sono netti ma caratterizzati da un'infinita
gradazione della possibilità degli eventi:
Per far
meglio comprendere tale gradazione, creare situazioni del tipo: -scegliere
l'urna dalla quale si ritiene che sia più probabile che venga
estratta la pallina di colore rosso:
OBIETTIVO PSI.3.
(2° CICLO) CONFRONTARE
IN SITUAZIONI DI GIOCO LE PROBABILITÀ DEI VARI EVENTI MEDIANTE
L'USO DI RAPPRESENTAZIONI OPPORTUNE. -Al
fine pervenire alla scoperta che la probabilità è rappresentata
dal rapporto tra il numero degli eventi favorevoli ed il numero
degli eventi equipossibili, creare situazioni di gioco che impegnino
a verificare, ad esempio, che su un grande numero di estrazioni, le
probabilità di estrarre:
(1/2 ¾ 0,50 ¾ 50%)
- (1/3 ¾ 0,33 ¾ 33,33%)
-
N.B.
È opportuno
che le estrazioni (in grande quantità: almeno 1000/2000 estrazioni
complessive) vengano effettuate da più gruppi di due persone,
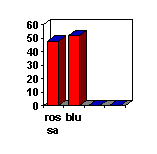
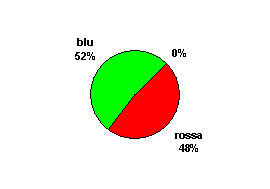
reimbussolando sempre la pallina estratta. I risultati delle
estrazioni possono essere rappresentati con istogrammi, diagrammi a
punti, a torta ecc.:
OBIETTIVO PSI.4
RAPPRESENTARE,
ELENCARE E NUMERARE TUTTI I POSSIBILI CASI IN SEMPLICI SITUAZIONI
COMBINATORIE; DEDURNE ALCUNE ELEMENTARI VALUTAZIONI DI PROBABILITÀ.
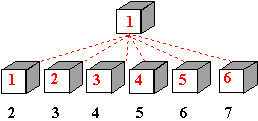
DISPOSIZIONE: modi di combinarsi in
successione di due o più oggetti distinti
-crea
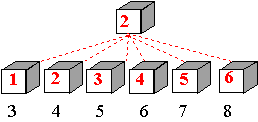
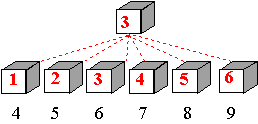
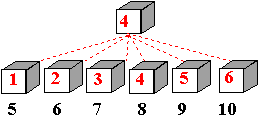
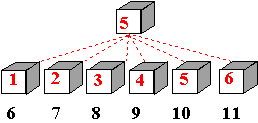
disposizioni significative di oggetti, come dai seguenti esempi: DUE ALUNNI
DUE DADI
DUE
SILLABE
TRE ALUNNI
TRE DADI
COMBINAZIONI Nelle
due disposizioni di due oggetti a due a due ciò che cambia è
l'ordine degli oggetti: se non si tiene conto dell'ordine e si
considerano solo gli oggetti, si può parlare di una sola combinazione.
-Creare situazioni significative di combinazione di
due o più elementi, come dai seguenti esempi: *formare tutte le possibili coppie di
due, tre, quattro alunni:
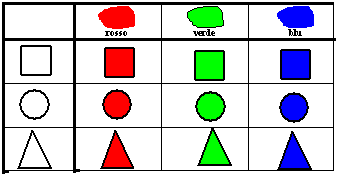
*abbinare
forme e colori in una tabella a doppia entrata, come la seguente:
Le somme
ottenute (spazio degli eventi) sono
36 e le loro presenze (distribuzione
delle frequenze) sono le seguenti:
BIBLIOGRAFIA DELL’AUTORE
UMBERTO TENUTA, Itinerari di Logica Probabilità
Statistica Informatica,
LA SCUOLA, BRESCIA, 1992, ill., pp. 344.
|
La pagina
- Educazione&Scuola©