|
|
|
M557 - ESAME DI STATO DI LICEO SCIENTIFICOCORSO DI ORDINAMENTOTema di: MATEMATICA PROBLEMA 1 In un piano, riferito ad un sistema di assi cartesiani ortogonali (Oxy),
è assegnata la curva k di equazione y = f(x), dove è:
a) Determinare per quali valori di x essa è situata nel
semipiano y>0 e per quali nel semipiano y<0. b) Trovare l’equazione della parabola passante per l’origine O
degli assi e avente l’asse di simmetria parallelo all’asse y,
sapendo che essa incide ortogonalmente la curva k nel punto di ascissa
-1 (N.B.: si dice che una curva incide ortogonalmente un’altra in
un punto se le rette tangenti alle due curve in quel punto sono
perpendicolari). c) Stabilire se la retta tangente alla curva k nel punto di ascissa
-1 ha in comune con k altri punti oltre a quello di tangenza. d) Determinare in quanti punti la curva k ha per tangente una retta
parallela all’asse x. e) Enunciare il teorema di Lagrange e dire se sono soddisfatte le
condizioni perché esso si possa applicare alla funzione f(x)
assegnata, relativamente all’intervallo
PROBLEMA 2 Si considerino le lunghezze seguenti:
[1]
dove a è una lunghezza nota non nulla ed x è una
lunghezza incognita.
a) Determinare per quali valori di x le lunghezze [1] si
possono considerare quelle dei lati di un triangolo non degenere. b) Stabilire se, fra i triangoli non degeneri i cui lati hanno le
lunghezze [1], ne esiste uno di area massima o minima. c) Verificato che per d) Indicato con ABC il triangolo di cui al precedente punto c), in
modo che BC sia il lato maggiore, si conduca per A la retta
perpendicolare al piano del triangolo e si prenda su di essa un punto
D tale che AD sia lungo a: calcolare un valore approssimato a
meno di un grado (sessagesimale) dell’ampiezza dell’angolo formato
dai due piani DBC e ABC. QUESTIONARIO 1. Il rapporto fra la base maggiore e la base minore di un trapezio
isoscele è 4. Stabilire, fornendone ampia spiegazione, se si può
determinare il valore del rapporto tra i volumi dei solidi ottenuti
facendo ruotare il trapezio di un giro completo dapprima intorno alla
base maggiore e poi intorno alla base minore o se i dati a
disposizione sono insufficienti.
2. Due tetraedri regolari hanno rispettivamente aree totali 3. Considerati i numeri reali a, b, c, d - comunque scelti - se
a>b e c>d allora: A) a+d > b+c; Una sola alternativa è corretta: individuarla e motivare
esaurientemente la risposta. 1. Si consideri la seguente proposizione: “La media aritmetica di
due numeri reali positivi, comunque scelti, è maggiore della loro
media geometrica”. Dire se è vera o falsa e motivare
esaurientemente la risposta.
2. Determinare, se esistono, i numeri a, b in modo che la seguente
relazione:
3. Si consideri la funzione:
Stabilire se ammette massimo o minimo assoluti nell’intervallo
4. Calcolare la derivata, rispetto ad x, della funzione f(x) tale
che:
f(x) =
5. La funzione reale di variabile reale
6. In un piano, riferito ad un sistema di assi cartesiani (Oxy),
è assegnato il luogo geometrico dei punti che soddisfano alla
seguente equazione:
Tale luogo è costituito da: A) un punto; Una sola alternativa è corretta: individuarla e fornire
un’esauriente spiegazione della risposta. 1. La funzione reale di variabile reale f(x), continua per ogni x,
è tale che: 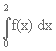 = a , = a , 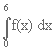 =
b , =
b ,
Determinare, se esistono, i valori a, b per cui risulta: 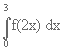 = ln 2 e = ln 2 e
______________________________
|
La pagina
- Educazione&Scuola©