ESAME DI STATO a.s. 2000-2001

La nuova struttura della prova scritta di matematica

La inadeguatezza della struttura tradizionale della prova scritta di matematica all'esame di Stato, da tempo segnalata dai docenti della disciplina e da esperti del mondo accademico e non, ha evidenziato l'esigenza di affrontare la questione e di prospettarne la soluzione.

Dopo un lungo dibattito che ha visto la attiva partecipazione di esperti universitari, rappresentanti delle diverse Associazioni scientifiche, di Ispettori tecnici del settore e docenti, si è giunti alla definizione del nuovo modello di prova che viene qui allegato.

Problemi e quesiti, predisposti in stretta coerenza con il piano di studi seguito, saranno impostati e formulati in modo agile e snello, al fine di rendere più agevole la scelta da parte del candidato.

La articolazione delle questioni sarà ispirata al criterio di una complessità graduale e a quello della non necessaria interdipendenza tra loro. Tali requisiti della prova, oltre a favorire il primo approccio del candidato alle questioni proposte, consentiranno alle Commissioni giudicatrici di saggiare lo studente su un più ampio spettro di argomenti e di definire criteri di revisione validi per una valutazione quanto più possibile oggettiva degli elaborati dei candidati.

Nulla è innovato per i corsi di Istituto magistrale in via di esaurimento.

CRITERI DI FORMULAZIONE

Corsi di:

• Ordinamento;
• Piano Nazionale Informatica;
• Progetti "Brocca";
• "Proteo" indirizzi: scientifico e scientifico-tecnologico

FINALITA'

Con riferimento alla matematica studiata nell'intero corso di studi la prova scritta è intesa ad accertare:

• le conoscenze specifiche
• le competenze nell'applicare le procedure e i concetti acquisiti
• le capacità logiche e argomentative.

STRUTTURA DELLA PROVA

Il testo è costituito da due problemi (articolati al loro interno in almeno tre quesiti, possibilmente indipendenti tra loro) e da un questionario contenente altri quesiti (da un minimo di 6 a un massimo di 10) riguardanti argomenti del programma.

La tipologia delle questioni poste è tale da offrire al candidato le più ampie opportunità di esprimere conoscenze, competenze e capacità acquisite nel corso degli studi.

Il candidato è tenuto a risolvere uno dei due problemi proposti a scelta e circa la metà dei quesiti del questionario.

DURATA DELLA PROVA E MATERIALE CONSENTITO

La durata massima della prova è di sei ore

Nel corso della prova è consentito soltanto l'uso di calcolatrici non programmabili

La soluzione di problemi e la risposta alle domande di un questionario sono le due tipologie di accertamento previste dalla nuova struttura della prova scritta di matematica: ecco in linea una proposta di modello della prova e un primo esempio di traccia.

Per superare la prova i candidati dovranno risolvere uno dei due problemi a scelta e rispondere correttamente alla metà dei quesiti del questionario.

STRUTTURA DEL TEMA DI MATEMATICA ALL’ESAME DI STATO

ESEMPIO 1

Il candidato risolva, a sua scelta, uno dei due problemi e 5 fra i 10 quesiti del questionario.

Problema 1

Problema 2

Questionario

____________________________

La durata della prova è di 6 ore e nel corso di essa è consentito soltanto l’uso di calcolatrici non programmabili.

Non è ammesso lasciare l’aula degli esami prima che siano trascorse tre ore dalla consegna della copia con le tracce.

Un esempio di prova di matematica all’esame di Stato nei Licei Scientifici di ordinamento

Il candidato risolva, a sua scelta, uno dei due problemi e 5 fra i 10 quesiti del questionario.

In un piano sono assegnate una circonferenza k di diametro AB, lungo 2, e una parabola p passante per A e avente per asse di simmetria il diametro perpendicolare ad AB. Si sa che la parabola divide il cerchio delimitato da k in due parti, la maggiore delle quali è 5 volte la minore.

Dopo aver riferito il piano della figura ad un conveniente sistema di assi cartesiani:

1) determinare l'equazione di k;

2) determinare l'equazione di p;

3) trovare le coordinate dei punti M ed N comuni alle curve k e p;

4) trovare le equazioni delle rette tangenti a p nei punti M ed N;

5) stabilire com'è situato rispetto alla circonferenza il punto in cui si secano le due rette tangenti trovate sopra.

Considerata una sfera di diametro AB, lungo 2, per un punto P di tale diametro si conduca il piano a perpendicolare ad esso e si ponga uguale ad x la lunghezza di AP.

1) Si calcoli in funzione di x la differenza d(x) fra il volume del cono avente altezza AP e base il cerchio sezione di a con la sfera e il volume del segmento sferico avente la medesima base e altezza PB.

2) Controllato che risulta:

d(x) = (2 - x) (2 x² – x - 2),

si studi la funzione d(x) e se ne disegni il grafico.

3) Si utilizzi questo grafico per calcolare i valori di x per i quali d(x) = k , dove k è un parametro reale assegnato.

4) Si trovi, in particolare, la posizione di P per cui d(x) è massima.

1. Considerata la successione di termine generale a_n = , dove:

f(n) = … +,

calcolare e, ricorrendo alla definizione, verificare il limite così trovato.

2. Sia f(x) una funzione reale di variabile reale, continua su tutto l’asse reale, tale che:

e .

Di ciascuno dei seguenti integrali:

, , , ,

dire se le condizioni assegnate sono sufficienti per calcolarne il valore e in caso di risposta affermativa qual è questo.

3. Si dimostri la formula della derivata del prodotto di due funzioni:

D[f(x)g(x)] = f ’(x)g(x) + f(x)g’(x) .

 

4. Si dimostri che il volume V di un segmento sferico ad una base, di raggio di base r ed altezza h è dato dalla seguente formula:

.

5. Si dimostri la formula che esprime la derivata, rispetto ad x, della funzione xⁿ, dove n è un intero qualsiasi non nullo.

6. Un trapezio rettangolo è circoscritto ad un semicerchio di raggio r in modo che la base maggiore contenga il diametro. Si determinino i lati del trapezio sapendo che il solido generato da esso quando ruota di un giro completo intorno alla base maggiore ha il minimo volume.

7. Si conducano le rette tangenti ad una parabola in due suoi punti distinti A e B. Si dimostri quindi la relazione che sussiste fra l’area del triangolo mistilineo delimitato dall’arco AB di parabola e dalle due tangenti suddette e l’area del segmento parabolico individuato dalla corda AB, nel caso particolare in cui la retta AB è perpendicolare all’asse di simmetria della parabola.

8. Si calcoli il valore del seguente integrale:

.

9. Si dimostri che ogni funzione f(x) = ax³ + bx² + cx + d , dove a,b,c,d sono valori reali con a¹ 0, ha un massimo e un minimo relativi oppure non ha estremanti.

10. In un piano cartesiano, l’insieme dei punti verificanti la condizione:

x y – 3 x + 5 y – 15 = 0

è costituito:

dai punti (5, 0) e (0, -3);

dai punti (-5, 0) e (0, 3);

dall’intersezione delle rette di equazioni x = -5 e y = 3;

dall’unione delle rette di equazioni x = -5 e y = 3;

da una figura diversa dalle precedenti.

Una sola risposta è corretta: individuarla fornendo una esauriente motivazione.

__________________________________

La durata della prova è di 6 ore e nel corso di essa è consentito soltanto l’uso di calcolatrici non programmabili.

Non è ammesso lasciare l’aula degli esami prima che siano trascorse tre ore dalla consegna della copia con le tracce.

ESEMPIO 2

Il candidato risolva, a sua scelta, uno dei seguenti problemi e dia le risposte a cinque quesiti del questionario:

PROBLEMA 1

Della parabola si hanno le seguenti informazioni, tutte localizzate nel punto  : , , .

Determinata la parabola, si scrivano le equazioni delle tangenti ad essa condotte per il punto P dell’asse y di modo che valga 60° l’angolo , essendo A e B i rispettivi punti di tangenza ;

accertato che il punto P ha ordinata , si scriva l’equazione della circonferenza passante per A, B e P ;

si calcolino le aree delle due parti in cui la circonferenza risulta divisa dall’arco di parabola di estremi A e B.

 

PROBLEMA 2

Vincenzo Viviani (1622-1703) nell’opera De Maximis et Minimis, data alle stampe nel 1659, avvertì la necessità di inserire un problema a cui aveva dato soluzione e che era stato oggetto di studio anche da parte di altri più noti e valenti matematici del tempo.

Il problema è il seguente :

" Dato un triangolo ABC, i cui angoli misurano ciascuno meno di 120°, trovare un punto X tale che la somma XA+XB+XC sia minima".

La soluzione di Viviani, trovata, egli dice, non senza iterati sforzi, è questa : X è il punto, interno al triangolo, che "vede" o proietta i lati AB, BC, CA, sotto angoli di 120°.

Il problema conserva inalterata la sua importanza in quanto se i vertici A, B e C rappresentano, ad esempio, tre villaggi o città che si vogliono collegare tra loro, ragioni di convenienza potrebbero consigliare di realizzare la rete stradale minima.

Il candidato:

localizzi il punto X nell’ipotesi semplificatrice che la retta passante per C e per il punto medio M del segmento AB sia perpendicolare a tale segmento ;

 

dimostri che il punto X che realizza il minimo appartiene al segmento CM ;

 

introdotto un sistema di coordinate tale che C sia l’origine e CM coincida con l’asse x positivo e indicate con (a,b) e (x,0) rispettivamente le coordinate di A e di X, dimostri che s(x)=XA+XB+XC è data dalla formula :

 

dimostri che se , s(x) assume il minimo in , mentre se , s(x) assume il minimo in  ;

interpreti geometricamente il risultato confrontandolo con l’enunciato e la soluzione, più generale, di Viviani.

 

 

 

 

 

 

QUESTIONARIO

illustrare il teorema di de L’Hôpital e applicarlo per dimostrare che:

Esempi di prova di matematica all’esame di Stato nei seguenti indirizzi:

- Scientifico PNI,

- Scientifico "Brocca",

- Scientifico-Tecnologico "Brocca"

ESEMPIO 1

Il candidato risolva, a sua scelta, uno dei due problemi e 5 fra i 10 quesiti del questionario.

PROBLEMA 1.

Nel piano, riferito ad un sistema monometrico di assi cartesiani ortogonali (Oxy), sono assegnati i punti: A(0, 2), B(1, 1), C(1, 0).

Trovare l’equazione della circonferenza g inscritta nel triangolo OAB.

Determinare le equazioni dell’affinità a che ha come punti uniti i punti O e C e trasforma il punto B nel punto A.

Calcolare l’area del triangolo CAA’, dove A’ è il punto trasformato di A nell’affinità a .

Stabilire se l’affinità a ha altri punti uniti, oltre ad O e C, e trovare le sue rette unite.

Stabilire quali, fra le rette unite trovate, risultano tangenti o esterne a g .

 

PROBLEMA 2.

Si consideri l’esperimento consistente nell’estrazione a caso di 5 palline, una dopo l’altra, senza reimbussolamento delle palline estratte, da un sacchetto contenente 90 palline numerate da 1 a 90, aventi tutte le stesse possibilità di uscita (gioco del Lotto).

Dire se è più probabile che, prescindendo dall’ordine di uscita, esca:

la cinquina di numeri "successivi" {1,2,3,4,5} o la cinquina di numeri "non successivi" {2,3,5,8,13};

- una qualunque cinquina di numeri "successivi" o una qualunque cinquina di numeri "non successivi".

Prese in esame le due seguenti proposizioni:

A: " La probabilità che il 2° numero estratto sarà il "90" è 1/89 " ,

B: " La probabilità che nei 5 numeri estratti ci sarà il "90" è 5/90 ",

stabilire quali delle seguenti implicazioni sono vere e quali no e fornire esaurienti spiegazioni:

(1) A ® B , (2) B ® A , (3) ® , (4) ® .

Supposto di puntare una determinata somma sull'uscita dei tre numeri 14, 8, 42 sulla "Ruota" di Napoli, calcolare la probabilità di vincita (fare un terno al Lotto). Se il gioco fosse equo e la puntata fosse di 5 Euri, quanto dovrebbe pagare lo Stato in caso di vincita del giocatore?

Supponendo di ripetere n volte l’esperimento considerato, calcolare la probabilità che il "90" esca, tra i 5 numeri estratti:

al più 5 volte;

per la prima volta proprio alla n-esima estrazione. Qual è il più piccolo valore di n per cui questa probabilità non supera 10^-10?

 

QUESTIONARIO

1. Considerata la successione di termine generale a_n = , dove:

f(n) = … +,

calcolare e, ricorrendo alla definizione, verificare il limite così trovato.

2. Sia f(x) una funzione reale di variabile reale, continua su tutto l’asse reale, tale che:

e .

Di ciascuno dei seguenti integrali:

, , , ,

dire se le condizioni assegnate sono sufficienti per calcolarne il valore e in caso di risposta affermativa qual è questo.

3. Sia f(x) una funzione reale di variabile reale tale che valgano le seguenti condizioni:

f (x₀) > 0 , f ’(x₀) > 0 , f "(x₀) = 0 ,

dove x₀ è un particolare valore reale.

Dire se tali condizioni non sono sufficienti a determinare l’andamento di f(x) in un intorno di x₀ e motivare esaurientemente la risposta.

 

4. Si dimostri che il volume V di un segmento sferico ad una base, di raggio di base r ed altezza h è dato dalla seguente formula:

.

5. Paolo e Giovanni sono due amici appassionati di tiro con l’arco: Paolo colpisce il centro del bersaglio nel 75% dei casi, Giovanni nell’80%. Decidono di fare una gara, nella quale tireranno a turno, ma è Giovanni che inizia a tirare.

Descrivere una procedura che permetta di calcolare la probabilità che Paolo vinca al lancio numero n tra quelli complessivamente effettuati dai due arcieri.

6. Un trapezio rettangolo è circoscritto ad un semicerchio di raggio r in modo che la base maggiore contenga il diametro. Si determinino i lati del trapezio sapendo che il solido generato da esso quando ruota di un giro completo intorno alla base maggiore ha il minimo volume.

7. Stabilire per quali valori del parametro reale k esiste una piramide triangolare regolare tale che k sia il rapporto fra il suo apotema e lo spigolo di base.

8. Si calcoli il valore del seguente integrale:

.

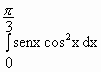9. Nel piano, riferito ad un sistema di assi cartesiani ortogonali, è assegnata l’affinità di equazioni:

.

Descrivere un algoritmo che risolva il problema di determinare l’equazione trasformata di quella di una data retta in base all’affinità considerata e di comunicare il risultato.

10. In un piano cartesiano, l’insieme dei punti verificanti la condizione:

x y – 3 x + 5 y – 15 = 0

è costituito:

dai punti (5, 0) e (0, -3);

dai punti (-5, 0) e (0, 3);

dall’intersezione delle rette di equazioni x = -5 e y = 3;

dall’unione delle rette di equazioni x = -5 e y = 3;

da una figura diversa dalle precedenti.

Una sola risposta è corretta: individuarla fornendo una esauriente motivazione.

 

__________________________________

La durata della prova è di 6 ore e nel corso di essa è consentito soltanto l’uso di calcolatrici non programmabili.

Non è ammesso lasciare l’aula degli esami prima che siano trascorse tre ore dalla consegna della copia con le tracce.

Esempi di prova di matematica all’esame di Stato nei seguenti indirizzi:

- Scientifico PNI,

- Scientifico "Brocca",

- Scientifico-Tecnologico "Brocca"

ESEMPIO 2

Il candidato risolva, a sua scelta, uno dei due problemi e 5 fra i 10 quesiti del questionario.

PROBLEMA 1

E’ assegnata la curva g di equazione

dove a è una costante positiva.

Il candidato :

studi e disegni il grafico di g  ;

verifichi in particolare che essa ammette due punti di flesso F₁ e F₂ di ascisse rispettive e

fornisca col metodo dei trapezi una stima dell’area della regione del piano delimitata dal grafico di g  sull’intervallo di estremi x₁ e x₂ e dal segmento F₁F₂ ;

dica se il risultato ottenuto rappresenti una stima per difetto o per eccesso del risultato esatto;

illustri la relazione che intercorre tra g  e la curva normale di Gauss utilizzata nella statistica.

 

 

PROBLEMA 2

Partendo dalla ben nota disuguaglianza

valida per qualsiasi valore reale di t, si stabiliscano, per mezzo di successive integrazioni, effettuate sull’intervallo , le disuguaglianze

Si diano, quindi, per mezzo della b), una valutazione per difetto e una per eccesso, dell’integrale :

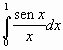(1)

Successivamente si interpreti geometricamente l’integrale (1) e si dimostri che .

QUESTIONARIO

1. Si dimostri, senza risolverla, che l’equazione :

ammette una e una sola radice reale.

 

Si valuti la radice dell’equazione proposta sopra con una precisione di due cifre significative mediante un qualsiasi procedimento iterativo e lo si codifichi in un linguaggio di programmazione conosciuto.

 

"p è la somma, espressa in radianti, degli angoli interni di un triangolo": si discuta la validità o meno di tale teorema in un contesto di geometria non euclidea.

Si dia una motivata risposta al seguente quesito:

«è più probabile che lanciando un dado due volte escano due numeri uguali, oppure che lanciandolo tre volte esca tutte e tre le volte un numero dispari ?»

 

Si chiarisca il significato di "sistema ipotetico-deduttivo" illustrandone sinteticamente le principali caratteristiche.

Si mostri che fra tutti i cilindri iscritti in un cono circolare retto ha volume massimo quello la cui altezza è la terza parte dell’altezza del cono.

 

Si esponga il teorema di de L’Hôpital e lo si applichi per dimostrare che, per n finito, , si ha : ;

 

Si determini la probabilità che in 6 lanci di un dado non truccato il numero 3 si presenti tre volte.

 

Si esponga il significato di variabile casuale X e di funzione (o distribuzione) di probabilità.

 

Si applichi la formula d’integrazione per parti per calcolare l’integrale definito:

__________________________________

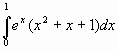
La durata della prova è di 6 ore e nel corso di essa è consentito soltanto l’uso di calcolatrici non programmabili.

Non è ammesso lasciare l’aula degli esami prima che siano trascorse tre ore dalla consegna della copia con le tracce.

Esempio di prova di matematica all’esame di Stato nei licei scientifici sperimentali (P.N.I. - Brocca scientifico ecc.)

Il candidato risolva, a sua scelta, uno dei due problemi e 5 fra i quesiti del questionario.

PROBLEMA 1.

E’ data, in un piano, riferito ad un sistema di assi cartesiani ortogonali Oxy, l’iperbole di equazione xy-x-2y=0 e siano r ed s i suoi asintoti, rispettivamente verticale ed orizzontale.

Il candidato:

1. tracci il grafico dell’iperbole;
2. scriva l’equazione della circonferenza passante per l’origine ed avente il centro nel punto d’incontro di r con l’asse delle ascisse;
3. constatato che, oltre che in O, le curve e s’incontrano in un ulteriore punto A, la cui ascissa è compresa tra 1 e 2, descriva una procedura che consenta di calcolare i valori approssimati, con un’approssimazione di , di e la codifichi in un linguaggio di programmazione conosciuto;
4. detto P un punto del semiasse negativo delle ascisse di coordinate (a,0), determini il volume V(a) del solido, ottenuto dalla rotazione di un giro completo intorno all’asintoto s, della parte finita di piano delimitata da , da s e dalle rette di equazione x=1 e x=a;
5. calcoli il

PROBLEMA 2.

Su un piano, riferito ad un sistema di assi cartesiani ortogonali Oxy, è data la linea di equazione .

Il candidato:

1. tracci la curva ;
2. detto A il punto di di ordinata massima relativa, B il punto, diverso da O, in cui interseca l’asse delle ascisse, P un punto del segmento OB, Q ed R le intersezioni della parallela per P all’asse delle ordinate rispettivamente con e con la retta OA, studi la funzione r(x) che esprime il raggio del cerchio di centro Q e passante per R;
3. determini in particolare il punto in cui r(x) raggiunge il valore massimo assoluto (nella ricerca degli estremi relativi si utilizzino i valori approssimati per eccesso a meno di 1/10 dei valori estremanti) e scriva l’equazione della circonferenza , contorno del corrispondente cerchio (centro ; raggio );
4. scriva l’equazione della curva ’, trasformata di mediante la trasformazione T di equazione , , e determini l’area della parte finita di piano da essa delimitata;
5. studi le caratteristiche di T e dica se è possibile determinare l’area della parte finita di piano delimitata da

QUESTIONARIO

1. E’ data una funzione f(x) la cui funzione derivata prima f ‘(x) ha per diagramma, in un piano riferito ad un sistema di assi cartesiani ortogonali Oxy, una semicirconferenza di centro C(0,1), raggio 2, passante per il punto A(0,-1).

Quali osservazioni si possono fare sull’andamento qualitativo del diagramma di f(x)?

 

2. Si considerino le uguaglianze:

e

Si dica se sono vere o false per ogni , giustificando le risposte.

3. Ricordando che la formula di Newton che dà la potenza n-esima di un binomio è:

si dica per quali valori di n il numero:

è positivo o negativo.

4. Ai tempi della repubblica di Venezia, l’elezione del doge avveniva tramite un sistema di sorteggi e ripescaggi tra un certo numero di persone, che nel nostro caso supporremo 100. In una prima fase sono sorteggiati 30 candidati tra i 100. In una seconda fase avvengono due ulteriori sorteggi: in uno 10 candidati sono scelti tra i 30, nell’altro 10 candidati sono ripescati tra i 70 inizialmente eliminati. In una terza fase, infine, un candidato è scelto come doge, sempre in base a sorteggio, tra i 20 candidati che hanno passato la seconda fase. Si dica qual è la probabilità che ognuno dei 100 candidati iniziali ha di divenire doge prima del primo sorteggio. Si determini, inoltre, qual è la probabilità di divenire doge per un candidato che abbia passato il primo turno, ossia tra i 30 selezionati, e la corrispondente probabilità per un candidato che non abbia passato tale sorteggio. Si confrontino le probabilità dei candidati prima e dopo il primo sorteggio.

5. E’ data la semisfera di centro O e sia la sua circonferenza massima. Si conducano due piani e , passanti per il raggio OP perpendicolare al piano di . Sia PQR il triangolo sferico, interno all’angolo acuto dei piani e , i cui vertici Q ed R sono le intersezioni della circonferenza con e . Si deduca, da quanto si può dire sulla somma degli angoli interni del triangolo PQR, che detto triangolo si può intendere come una figura di un modello di geometria non euclidea.

 

6. Avvalendosi della definizione di derivata come limite del rapporto incrementale al tendere dell’incremento della variabile indipendente a zero, si dimostri che la derivata della funzione
   è .

 

7. Si dia un esempio di funzione f(x) a cui in un intervallo

8. Su un piano è tracciata una circonferenza di raggio r. Per un punto A di si conduca una semiretta perpendicolare ad e su di essa si consideri il punto V tale che VA = h. Dopo aver dimostrato che la sezione ’del cono , di base la circonferenza e vertice V, con un piano ’, parallelo ad è una circonferenza, si calcoli, avvalendosi di un integrale definito, il volume di.

 

9. In un piano, riferito ad un sistema di assi cartesiani ortogonali Oxy, si disegni il grafico di una funzione avente come asintoti verticali le rette di equazione x=1 e x=-1 e come asintoto orizzontale la retta di equazione y = . Si determini, inoltre, una funzione il cui grafico soddisfi le condizioni predette.

 

1. Si consideri la famiglia di curve di equazione y=f(x), essendo f(x) =

_________________________________

La durata della prova è di 6 ore e nel corso di essa è consentito soltanto l’uso di calcolatrici non programmabili.

Non è ammesso lasciare l’aula degli esami prima che siano trascorse tre ore dalla consegna della copia con le tracce.