Il problema cruciale per la moderna crittografia risiede nella chiave che deve essere modificata e trasmessa assai spesso al fine di proteggere la comunicazione da possibili spie. La cosidetta crittazione a chiave pubblica risolve il problema con due principali procedimenti i quali, come vedremo, si basano sulla funzione resto o modulo che è sostanzialmente unidirezionale.
La funzione modulo fornisce z il quale è il resto di x diviso per y, e si scrive così

z = (x mod y)

Questo risultato è facilmente ottenibile, mentre la funzione che opera nella direzione inversa, cioè procura il valore x partendo da z e da y, è di fatto irrealizzabile, specie se i numeri in gioco hanno centinaia di cifre.
Chiariamo il concetto di funzione unidirezionale con la seguente tabellina che riporta le potenze di due. Nell'ultima riga ci sono i resti della loro divisione per 11. Si nota che le potenze sono regolarmente crescenti mentre i resti hanno un andamento del tutto casuale. Risalire dai resti ai dividendi è praticamente impossibile.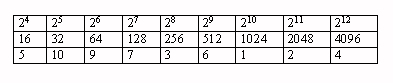

Nel 1976, due giovani americani Whitefield Diffie e Martin Hellman trovarono che si può creare una chiave identica e segreta presso i due interlocutori senza doverla spedire.

Facciamo il caso di Alice e Bruno che pubblicamente notificano di lavorare con il numero primo p e l'intero n (1<n<p). Essi procedono nel modo seguente. Alice sceglie il proprio numero segreto a e calcola A=(n^a mod p). Contemporaneamente Bruno sceglie b, anche questo segreto, e calcola  B=(n^b mod p). Alice e Bruno si scambiano i risultati. Infine Alice calcola (B^amod p) e Bruno calcola (A^bmod p) che danno lo stesso valore, infatti: 

(B^amod p) = [(n^a)^bmod p] = [(n^b)^amod p] =(A^bmod p) = k

I due hanno in mano la chiave segreta k che non è stata trasmessa da nessuno e quindi è assai sicura. Dopo aver intercettato nella rete n e p, e poi A e B, nessuno può trovare k senza conoscere a oppure b. 

Come esempio numerico supponiamo che in privato Alice scelga a=3 e Bruno b=6. I valori n e p sono rispettivamente 7 ed 11 e pubblicamente noti. Alice calcola 7³= 343 che diviso per 11 da 2. Bruno invece calcola 7⁶=117649 che diviso per 11 da come resto 4. I due interlocutori si scambiano i risultati. Alice prende il numero 4 appena ricevuto e calcola 4³=64 che diviso per 11 da 9. Bruno calcola 2⁶=64 il quale diviso per 11 da 9. Entrambi ottengono k=9 che adottano come chiave segreta.

Ronald Rivest, Adi Shamir e Leonard Adleman nel 1977 trovano un'altra soluzione applicando sempre la funzione modulo alla crittografia. L'algoritmo RSA (dalle loro iniziali) permette di crittare e decrittare con due chiavi diverse: la prima è pubblica e la seconda è segreta. Il metodo, chiamato "a chiave asimmetrica", è oggi ampiamente usato in Internet. Due ricercatori del controspionaggio inglese, James Ellis Clifford Cocks, sembra che l'avessero scoperto in precedenza, ma avendolo tenuto segreto ne hanno perduto la paternità.

L'algoritmo RSA vuole che il messaggio scambiato sia trattato come un numero, ma questo non è affatto un problema perché qualsiasi testo, suono e immagine è formato da una stringa di bit che si può assimilare ad un numero. Per vedere come funziona, facciamo il caso di un venditore in Internet che stabilisce una chiave formata da due grandi numeri naturali: N, E, che spedisce pubblicamente all'acquirente. Questo tratta il proprio messaggio (ad esempio un ordine di acquisto) come numero binario M e calcola M^E, divide il risultato per N ed infine trova il resto C che spedisce in modo pubblico al venditore.
Come fa il venditore a decrittare C, ed ottenere M?
Il ricevente sa che N è il prodotto di due numeri primi p e q, perché è stato proprio lui a scegliere N. E' il dato segreto che conosce soltanto il venditore nel nostro esempio, nessun altro nella rete ne è al corrente.
Il venditore, una volta acquisito il valore C dall'acquirente, produce il numero D come resto di 1/E diviso per (p-1)(q-1)

D=[1/E   mod   (p-1)(q-1)]

Quindi eleva C alla D, lo divide per N ed ottiene il resto: questo resto è il messaggio originale M !

Facciamo un esempio numerico ovviamente in base decimale. Supponiamo che quello che scrive l'acquirente corrisponda al numero 3314. In precedenza dal venditore gli erano stati forniti pubblicamente E=11 ed N=11023. L'acquirente calcola

C=(3314¹¹mod 11023)=10260

e lo spedisce al venditore il quale sa che N è il prodotto dei numeri primi p=73 e q=151:

(73 *151) = 10023 = N

Soltanto lui conosce questi valori e calcola:

(73-1)(151-1)=10800

Quindi trova:

D=(1/11mod 10800)=5891

Con questo risultato arriva a ricostruire il valore vero che l'acquirente gli ha inviato grazie alla formula finale:

M=(C^D mod N)=
= (10260⁵⁸⁹¹mod 11023)=3314     !!!

La forza del sistema RSA è nei numeri primi p, q che hanno centinaia di cifre. Molti matematici hanno tentato di risalire a loro avendo in mano i dati scambiati pubblicamente. Ma i fallimenti hanno convinto dell'alta affidabilità di RSA.
 

anno 2004