LE SFUMATURE
DELLA FILOSOFIA E DELLA TECNOLOGIA
La logica fuzzy trova significativi antecedenti nelle logiche multivalenti e nel calcolo della probabilità, anche se gli specialisti tendono a smentire tali legami al fine di evidenziarne i lati originali di questo studio.
Loro definiscono la logica fuzzy come teoria di insiemi fuzzy cioè teoria di insiemi che hanno contorni indistinti. Cominciamo dunque a spiegare che cos'è un insieme fuzzy.
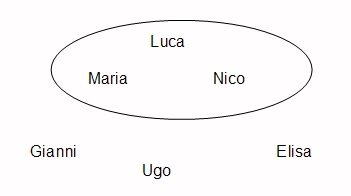
Un insieme è un gruppo di elementi che hanno qualcosa in comune. Mettiamo un insieme persone dai capelli neri: nella teoria degli insiemi classica una persona se è bruna appartiene all'insieme altrimenti no. Non esistono vie di mezzo. Ad esempio Luca, Maria e Nico sono mori di capelli ed appartengono all'insieme X, mentre Gianni, Elisa ed Ugo che non hanno i capelli neri non appartengono all'insieme X.
La logica fuzzy è più
raffinata. Al posto del brutale 'appartiene/non-appartiene', stabilisce
un
grado di appartenenza
di ciascun elemento all'insieme mediante un valore che va da 0 ad 1.
Nel nostro caso a Luca ed a Maria che hanno capelli assolutamente
neri, si dà 100%, Nico con qualche capello bianco ha 95%. Elisa che è bionda
ha 0%, mentre Gianni ed Ugo, castani scuri, hanno grado di appartenenza
all'insieme fuzzy X pari
al
50%.
L'appartenenza
di un elemento qualsiasi ad un insieme si esprime spesso con una frase, e la
logica fuzzy presenta lati originali anche da questo lato.
Nella logica
bivalente una proposizioneè vera oppure è falsa
(tertium non datur). Non ci sono altri possibili valori oltre al vero ed al falso ed
inoltre non è possibile che una proposizione sia contemporaneamente vera e
falsa. La logica fuzzy che riconosce varie gradazioni di appartenenza,
prevede una gamma continua di valori tra
l'assolutamente vero e l'assolutamente falso. Esempio la frase
"Maria ha i capelli neri "
è vera all'100%, mentre
"Nico ha i capelli neri "
E' vera al 95% perchè Nico ha un pò di capelli bianchi.
La logica fuzzy non è
bivalente
ma
multivalente
e grazie a questa sua qualità permette di risolvere significativi problemi
di logica.
La
seguente proposizione, nota già agli antichi filosofi greci, presenta un
evidente paradosso che è irrisolvibile nella logica bivalente:
"Il cretese Epimenide afferma che ogni cretese è bugiardo"
Sia se fosse vera sia se fosse falsa, contiene una palese
contraddizione.
Quando invece consideriamo la frase nell'ottica sfumata, gli possiamo
assegnare un valore parziale di verità ed il paradosso svanisce. In questo
modo il problema viene elegantemente risolto dalla logica fuzzy.
A che serve in pratica la logica fuzzy?
Il miglior campo applicativo lo trova negli apparati di
controllo che lavorano con regole del tipo:
Se A allora B
La condizione A verrebbe malamente espressa in modo assoluto, esempio:
Se "la temperatura è 15 °C" allora "accendi il riscaldamento".
Invece viene espressa in modo più realistico in questo modo:
Se "la temperatura è bassa" allora "accendi il riscaldamento".
Se "le azioni Y sono in rialzo" allora "compera le azioni Y".
Se "il respiro peggiora" allora "somministra ossigeno al malato".
"Temperatura bassa" non equivale ad un solo valore, ma a molti valori tarati a secondo delle situazioni. Così pure "Azioni Y in rialzo" e "Il respiro peggiora" sono condizioni articolate.
I sistemi di controllo fuzzy sono programmati via software, anche usando
linguaggi tradizionali (es. Assembler).
Nel 1986
venne sviluppato il primo chip che introdusse la logica fuzzy a livello
hardware. Quando anche i circuiti sono predisposti alla logica sfumata, le prestazioni del sistema di controllo
(cioé velocità di esecuzione, semplicità del codice ecc.) sono molto elevate ed i vantaggi sono molto apprezzati
operando in tempo reale.